RAG in Practice
What is Retrieval-Augmented Generation?
Retrieval-Augmented Generation (RAG) helps Large Language Models (LLMs) like ChatGPT give more accurate answers by connecting them to external knowledge sources.
LLMs are great at generating text, but they sometimes "hallucinate" or provide inaccurate information. RAG fixes this by using mathematical techniques like vector embeddings and cosine similarity metrics to connect LLMs to the relevant sections of external databases.
This makes the results more reliable and useful.
How RAG Works
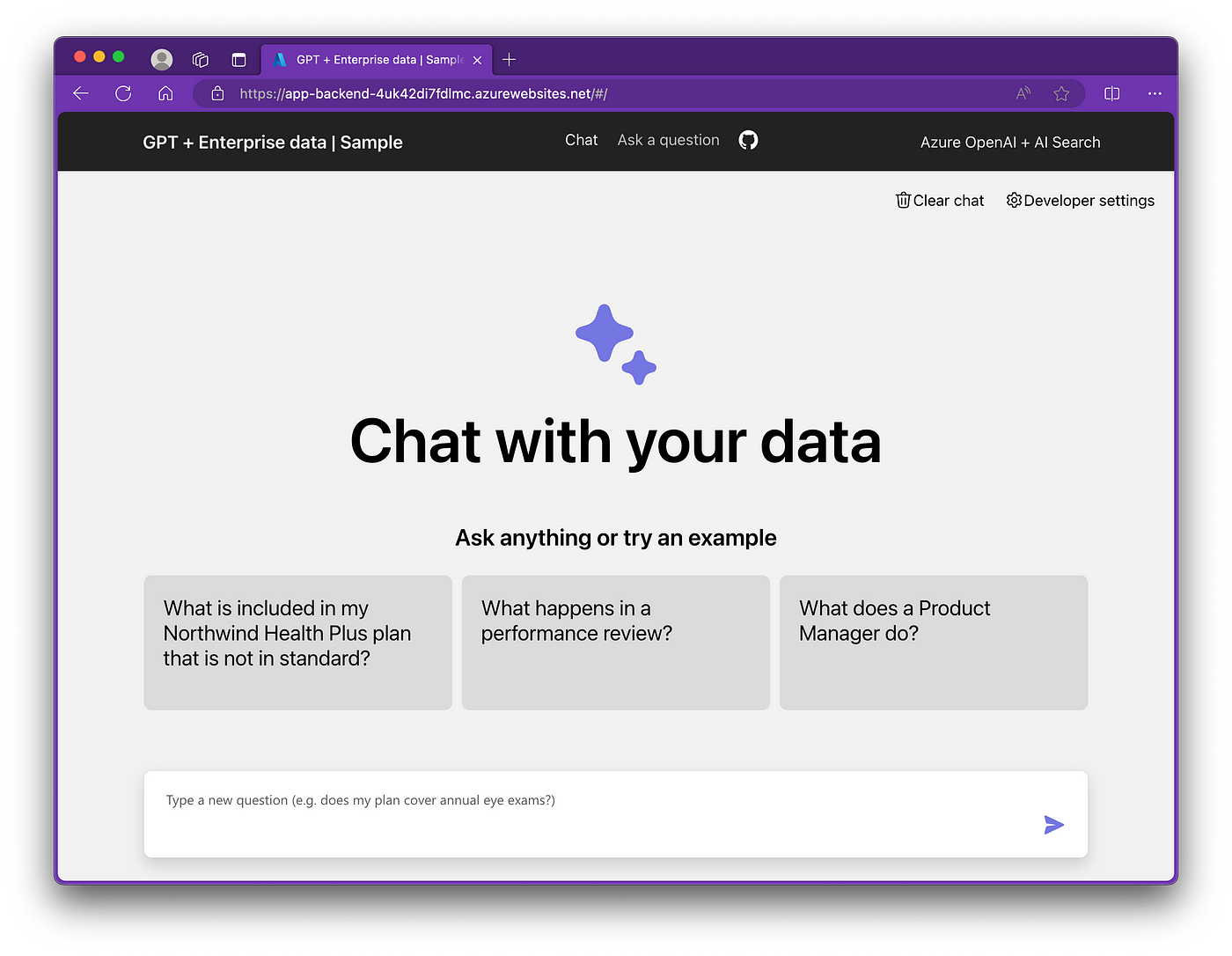
RAG systems follow three main steps:
- Retrieval: The system searches for relevant information by converting both the query and potential answers into mathematical vectors. It then calculates which vectors are closest in multi-dimensional space using cosine similarity.
- Augmentation: The retrieved information is added to your question using ranking algorithms to prioritize the most relevant content. This can be a simple rule-based algorithm or a more complex ML model.
- Generation: The model uses probability distributions to predict the best response, considering both its training and the retrieved context. This mathematical approach ensures the most relevant information is used in the final answer.
RAG systems can work with different types of data, like plain text, PDFs, or even databases. For example, when working with a PDF, the system might extract tables or use code to query the data.
Other Methods to Improve LLMs
RAG is not the only way to improve LLMs. Here are three common methods:
- Prompt Engineering: Involves writing better questions or prompts to guide the model. For example, adding "Explain it step by step" to a math question.
- Fine-Tuning (FT): Involves retraining the model with new data to improve specific skills. For instance, training the model with medical data to answer health-related questions.
- RAG: Uses external sources to give the model real-time access to new information.
Each method has its strengths. Prompt engineering is quick and simple. Fine-tuning creates highly specialized models. RAG is flexible and provides up-to-date information.
The Math Behind RAG
1. Embedding Spaces
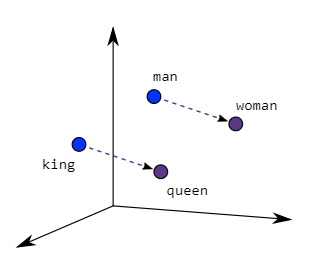
RAG works by converting text into vectors (embeddings) in a multi-dimensional space using algorithms like Word2Vec.
Word2Vec, for example, is a two-layer neural network that processes text by taking in batches of raw textual data, analyzing the relationships between words, and producing a vector space with several hundred dimensions. In this space, similar words or phrases are represented as vectors that are close together.
Word2Vec operates using two main architectures:
- CBOW (Continuous Bag of Words): Predicts a target word from its context words. For example, given the sentence "The cat sits on the mat", CBOW might try to predict "sits" from ["The", "cat", "on", "the", "mat"].
- Skip-gram: The reverse of CBOW - predicts context words from a target word. Using the same example, Skip-gram would try to predict ["The", "cat", "on", "the", "mat"] from the word "sits".
Both architectures learn word relationships by analyzing how words appear together in text. The key principle is that words appearing in similar contexts should have similar vector representations. For instance, "king" and "queen" might have similar vectors because they often appear in similar contexts about royalty.
For instance, the phrase "tall building" might be represented as [0.8, 0.3, 0.9], while the word "skyscraper" could become [0.9, 0.2, 0.8]. The closeness of these vectors in the multi-dimensional space shows their semantic similarity. This numerical representation enables mathematical comparison of text similarity using metrics like cosine similarity. By leveraging such embeddings, RAG can efficiently retrieve and compare relevant data.
-660.png)

2. Similarity Measures in RAG
While RAG commonly uses cosine similarity, there are several ways to measure vector similarity:
- Euclidean Distance: Measures straight-line distance between vectors
- Manhattan Distance: Measures distance along axes (like city blocks)
- Jaccard Similarity: Compares set intersection to union
- Minkowski Distance: Generalization of Euclidean and Manhattan
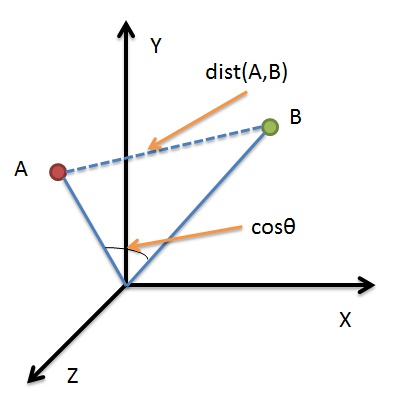
- Cosine Similarity: Measures angle between vectors
Cosine Similarity
Cosine similarity is particularly useful for text similarity because it's independent of vector magnitude, focusing on direction.
Formula:
cos(θ) = (v·u) / (||v|| ||u||)
where:
- • v·u = dot product of vectors
- • ||v|| = magnitude of vector v
- • ||u|| = magnitude of vector u
Example Calculation
For vectors:
x = [3, 2, 0, 5]
y = [1, 0, 0, 0]
Steps:
- 1. Dot product: (3×1 + 2×0 + 0×0 + 5×0) = 3
- 2. ||x|| = √(3² + 2² + 0² + 5²) = 6.16
- 3. ||y|| = √(1² + 0² + 0² + 0²) = 1
- 4. Similarity = 3 / (6.16 × 1) = 0.49
Interpretation
- • Score of 1: Vectors point in same direction (identical)
- • Score of 0: Vectors are perpendicular (unrelated)
- • Score of -1: Vectors point in opposite directions
3. Ranking Algorithms
When a query vector (user input) is compared against a database of vectors, RAG follows these steps:
- Compute the similarity scores using cosine similarity
- Sort theresults in descending order (highest similarity first)
- Return the top k results as most relevant
Normalization and Softmax
The above was a simple rule-based algorithm. If we want to refine the similarity scores, RAG can use:
Softmax Function:
P(document_i) = exp(score_i) / Σ exp(score_j)
The softmax function converts similarity scores into probabilities, which can be useful when you want probabilistic rankings rather than raw similarity scores.

The Math Behind LLMs
Since RAG supports LLMs, let's review the math behind large language models as well.
1. Attention Mechanism
The attention mechanism is a key component of transformers, calculating how much focus to put on different parts of the input. The formula for attention uses the softmax function we just described:
Where Q (Query), K (Key), and V (Value) are matrices, and d_k is the dimension of the keys. This allows the model to weigh the importance of different words in context.
2. Loss Functions
LLMs typically use cross-entropy loss for training, which measures the difference between predicted and actual word probabilities:
Where y_true is the actual word distribution and y_pred is the model's prediction. This helps the model learn to predict the next word accurately.
3. Position Encoding
To maintain word order information, transformers use positional encodings:
This adds position information to each word embedding, helping the model understand word order in sentences.
Examples of RAG in Action
- Technical Documentation: When searching through code documentation:
- Embeddings capture both natural language and code syntax
- Distance metrics find similar code examples
- Ranking ensures the most relevant examples appear first
- Personalized Relevant Guidance: Future U!!
You can take a look at the process used to develop Future U in the section.